प्रकाशगति का मापन

प्रकाशगति का मापन कैसे किया गया ? यह प्रश्न कई बार पुछा जाता है और यह एक अच्छा प्रश्न भी है। 17 वी सदी के प्रारंभ मे और उसके पहले भी अनेक वैज्ञानिक मानते थे कि प्रकाश की गति जैसा कुछ नही होता है, उनके अनुसार प्रकाश तुरंत ही कोई कोई भी दूरी तय कर सकता है। अर्थात प्रकाश शून्य समय मे कोई भी दूरी तय कर सकता है।

गैलेलियो का प्रयास

लेकिन गैलेलियो गैलीली इस से सहमत नही थे तथा उन्होने प्रकाशगति मापने के लिये प्रयोग करने का निश्चय किया। वे और उनके सहयोगी ने ढक्कन वाली लालटेन ली और वे एक दूसरे से एक मील दूरी पर दो पहाड़ीयों के शिर्ष पर जा पहुंचे। गैलेलियो ने अपने सहयोगी को निर्देश दिया था कि जैसे ही वह अपनी लालटेन का ढक्कन हटायेंगे, सहयोगी उनकी लालटेन के प्रकाश को देखकर अपनी लालटेन का ढक्कन हटायेगा। गैलेलीयो दूसरी पहाड़ी के शिर्ष से आनेवाले प्रकाश द्वारा लगनेवाले समय का मापन करेंगे।

इस समय को दूरी से विभाजित करने पर प्रकाश गति मिल जायेगी। यह प्रयोग बूरी तरह असफल रहा। कारण सरल था, प्रकाशगति इतनी अधिक है कि एक मील की दूरी तय करने उसे अत्यंत नगण्य समय लगा, केवल 0.0000005 सेकंड! गैलेलियो के पास समय के इतने छोटे भाग के मापन के लिये कोई उपकरण ही नही था।

अर्थात आपको प्रकाशगति के मापन के लिये लंबी दूरी वाले प्रयोग करने होंगे, लाखो करोड़ो मील दूरी के! इतनी विशाल दूरी के प्रयोग कैसे किये जाये ?

ओल रोमर का प्रयास

हब्बल अंतरिक्ष वेधशाला द्वारा लिया गया बृहस्पति, चंद्रमा आयो तथा आयो की छाया का चित्र।

1670 मे एक डेनिश खगोल वैज्ञानिक ओल रोमर (Ole Roemer) बृहस्पति के चंद्रमा आयो(Io) का निरीक्षण कर रहे थे। चित्र मे बृहस्पति पर दिखायी दे रहा काला धब्बा आयो की छाया है। आयो बृहस्पति की एक परिक्रमा करने मे 1.76 दिन का समय लेता है और परिक्रमा मे लगने वाला यह समय हमेशा समान रहता है। रोमर ने सोचा कि वे आयो की गति की सटिक गणना कर सकते है। लेकिन वह उस समय आश्चर्यचकित रह गये जब उन्होने पाया कि यह चंद्रमा वर्ष मे हमेशा उसी समय पर दिखायी नही देता था, कभी वह समय से पहले दिखायी देता था, कभी वह समय से पहले दिखायी देता था।
यह विचित्र था, आयो बृहस्पति परिक्रमा मे कभी तेज, कभी धीमे क्यों करता था ?

रोमर परेशान हो गये, कोई भी इसका संतोषजनक उत्तर नही दे पा रहा था। लेकिन रोमर ने अचानक पाया कि आयो जब तेजी से परिक्रमा करता है उस समय पृथ्वी बृहस्पति के समीप होती है, और जब वह धीमे परिक्रमा करता है तब पृथ्वी बृहस्पति से दूर होती है।

रोमर ने सोचा कि यह प्रकाश गति से संबधित होना चाहिये, लेकिन कैसे रोमर समझ नही पा रहे थे।

रोमर ने बाद मे सोचा कि यदि प्रकाश अनंत गति से यात्रा नही करता है और उसकी गति सीमीत है, इस स्थिति मे प्रकाश को बृहस्पति से पृथ्वी तक पहुचने मे कुछ समय लगता होगा। मान लेते है कि यह समय x मिनट है। जब आप बृहस्पति को किसी दूरबीन से देखते है तब हम उससे निकलने वाले प्रकाश को x मिनट बाद देख रहे होते है, अर्थात बृहस्पति और उसके चंद्रमाओं की x मिनट पुरानी छवि देख रहे होते है।

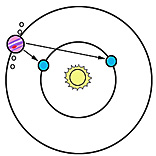इसका अर्थ यह है कि जब बृहस्पति पृथ्वी से दूर होता है, तब उसके प्रकाश को पृथ्वी तक पहुंचने मे अधिक समय लगता है, और बृहस्पति के पृथ्वी के समीप होने पर यह समय कम होता है। इसका अर्थ यह है कि आयो की बृहस्पति की परिक्रमा का समय एक ही है, लेकिन बृहस्पति की पृथ्वी से दूरी जब कम होती है आयो पहले दिख जाता है, जबकि दूरी अधिक होने पर वह बाद मे दिखायी देता है।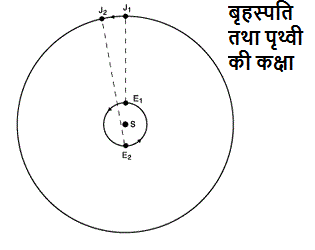

रोमर ने प्रकाशगति की गणना बृहस्पति के चंद्रमा आयो के ग्रहण मे लगने वाले समय से की थी। इस चित्र मे S सूर्य है, E1 पृथ्वी है जब वह बृहस्पति J1 के समीप होती है। छह महिने पश्चात E2 स्थिति मे पृथ्वी सूर्य के दूसरी ओर है तथा बृहस्पति J2 पृथ्वी से अधिकतम दूरी पर है।
जब पृथ्वी E2 पर होती है बृहस्पति से उत्सर्जित प्रकाश को पृथ्वी की कक्षा के तुल्य दूरी अधिक तय करनी होती है। इस अधिक दूरी को तय करने मे लगने वाले समय तथा पृथ्वी की कक्षा के व्यास के आधार पर रोमर ने प्रकाश गति की गणना की थी।

रोमर ने पाया कि आयो के दिखायी देने के समय के अंतर तथा बृहस्पति और पृथ्वी के मध्य दूरीयों मे आने वाले अंतर से प्रकाशगति की गणना कर सकते है। रोमर ने गणना की और प्रकाशगति को 210,000 किमी/सेकंड पाया। वर्तमान विज्ञान के अनुसार प्रकाशगति लगभग 300,000 किमी/सेकंड है।

बाद के वर्षो मे बेहतर उपकरण और तकनीको के अविष्कार के फलस्वरूप प्रकाशगति मे मापन मे सटिकता आते गयी और प्रकाशगति का मापन सटिक होते गया। वर्तमान मे उपलब्ध तकनीक से हम अत्यंत परिशुद्ध मापन कर सकते है। उदाहरण के लिये अंतरिक्षयात्री चंद्रमा पर एक चट्टान पर एक दर्पण छोड़्कर आये है। हम उस दर्पण पर लेजर से निशाना लगा कर लेजर प्रकाश के चंद्रमा से आने जाने का समय ज्ञात कर सकते है जोकि 2.5 सेकंड है। इस विधि से भी प्रकाश की गति की गणना करने पर मूल्य 300,000 किमी/सेकंड प्राप्त होता है। चंद्रमा पर दर्पण रख कर प्रकाशगति ज्ञात करने का आईडीया भी गैलेलीयो का था।

सभी विद्युत-चुंबकीय विकिरण जैसे रेडीयो तरंग, माइक्रोवेव भी इसी गति से यात्रा करते है।

प्रकाशगति की गणना का इतिहास

वर्ष	वैज्ञानिक	विधि	परिणाम(किमी/सेकंड)	त्रुटि
1676	ओल रोमर (Olaus Roemer)	बृहस्पति के उपग्रह	214,000
1726	जेम्स ब्रेडली (James Bradley)	खगोलिय विक्षेप(Stellar Aberration)	301,000
1849	अर्मांड फ़िजेउ(Armand Fizeau)	दांत वाले चक्र(Toothed Wheel)	315,000
1862	लीओन फ़ोकाट(Leon Foucault)	घूर्णन करते दर्पण(Rotating Mirror)	298,000	+-500
1879	अलबर्ट माइकल्सन(Albert Michelson)	घूर्णन करते दर्पण(Rotating Mirror)	299,910	+-50
1907	डोर्सी रोजा(Rosa, Dorsay)	विद्युत चंबकिय स्थिरांक(Electromagnetic constants)	299,788	+-30
1926	अलबर्ट माइकल्सन(Albert Michelson)	घूर्णन करते दर्पण(Rotating Mirror)	299,796	+-4
1947	एसेन, गार्डन-स्मिथ(Essen, Gorden-Smith)	केविटि रेजोनेटर(Cavity Resonator)	299,792	+-3
1958	के डी फ़्रूमे(K. D. Froome)	रेडीयो इन्टर्फ़ेरोमिटर(Radio Interferometer)	299,792.5	+-0.1
1973	एवानसन (Evanson et al)	लेजर(Lasers)	299,792.4574	+-0.001
1983		वर्तमान मूल्य	299,792.458